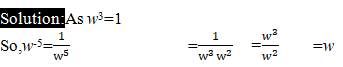If 1,w, w2 are the cube roots of unity, then
1+w=…….
a) 0
b)w
c)w2
d)-w2
Solution: 1+w+w2=0 1+w=-w2
If 1,w,w2 are the cube roots of unity, then w+w2=…….
a) 1
b)-1
c)w2
d)-w2
Solution:1+w+w2= 0 w+w2=-1
If w is complex cube root of unity, then w7 =
a) w
b) –w
c)w2
d)-w2
Solution:As w3=1 So,w7=w3.w3.w
=1.1.w =w
If w is complex cube root of unity, then w23 =
a)w
b) – w
c)w2
d) – w2
Solution:As w3=1
So,w23=(w3)7.w2 =(1)3.w2 =w2
If w is complex cube root of unity, then w63 =
a)w
b)1
c)w2
d) – w2
Solution: As w3=1
So,w63=(w3)21 =(1)63 =1
If w is complex cube root of unity, then w-5 =
a)w
b) 1
c)w2
d)w-2